Rounding in depth

library(scrutiny)

Large parts of scrutiny are about rounding. This topic is more diverse and variegated than one might think. “Rounding” is often taken to simply mean rounding up from 5, and although that’s wrong, it doesn’t make much of a difference most of the time.

One place where it does matter is in reconstructing the rounding procedures that others used, claim to have used, or are alleged to have used. In short, rounding and all its details matter for error detection.

This vignette goes into depth on scrutiny’s infrastructure for reconstructing rounding procedures and results from summary statistics. All of that is essential for the package: it is a precondition for translating assumptions about the processes behind published summary data into a few simple, higher-level function calls. Some of the functions presented here might be useful beyond the package, as well.

Feel free to skip the more theoretical parts if your focus is on the code. See vignette("rounding-options") for a list of possible values of the rounding argument in scrutiny functions.

Overview

Base R’s round() function is surprisingly sophisticated. This distinguishes it from simpler rounding procedures, such as rounding up from 5. For this very reason, however, it can’t be used to reconstruct the rounding procedures of other software programs. This is the job of scrutiny’s rounding functions.

First, I will present reround(), a general interface to reconstructing rounded numbers, before going through the individual rounding functions. I will also discuss unround(), which works the reverse way: It takes a rounded number and reconstructs the bounds of the original number, taking details about the assumed rounding procedure into account. Finally, I will take a closer look at bias from rounding raw numbers.

Reconstruct rounded numbers with reround()

None of the error detection techniques in scrutiny calls the individual rounding functions directly. Instead, all of them call reround(), which mediates between these two levels. reround() takes the vector of “raw” reconstructed numbers that were not yet rounded in the way that’s assumed to have been the original rounding procedure. Its next argument is digits, the number of decimal places to round to.

The remaining three arguments are about the rounding procedure. Most of the time, only rounding will be of any interest. It takes a string with the name of one of the rounding procedures discussed below.

Here is an example for a reround() call:

reround(x = c(5.812, 7.249), digits = 2, rounding = "up")
#> [1] 5.81 7.25

The two remaining arguments are mostly forgettable: They only concern obscure cases of rounding with a threshold other than 5 (threshold) and rounding such that the absolute values of positive and negative numbers are the same (symmetric). Ignore them otherwise.

Rounding procedures in detail

Up and down

round_up() does what most people think of as rounding. If the decimal portion to be cut off by rounding is 5 or greater, it rounds up. Otherwise, it rounds down.

round_up(x = 1.24, digits = 1)
#> [1] 1.2

round_up(x = 1.25, digits = 1)
#> [1] 1.3

round_up(x = 1.25)  # default for `digits` is 0
#> [1] 1

Rounding up from 5 is actually a special case of round_up_from(), which can take any numeric threshold, not just 5:

round_up_from(x = 4.28, digits = 1, threshold = 9)
#> [1] 4.2

round_up_from(x = 4.28, digits = 1, threshold = 1)
#> [1] 4.3

These two functions have their mirror images in round_down() and round_down_from(). The arguments are the same as in round_up():

round_down(x = 1.24, digits = 1)
#> [1] 1.2

round_down(x = 1.25, digits = 1)
#> [1] 1.2

round_down(x = 1.25)  # default for `digits` is 0
#> [1] 1

round_down_from(), then, is just the reverse of round_up_from():

round_down_from(x = 4.28, digits = 1, threshold = 9)
#> [1] 4.3

round_down_from(x = 4.28, digits = 1, threshold = 1)
#> [1] 4.2

Rounding up implements this formula:

$$\frac{\lfloor x(10^d) +1 - \frac{t}{10} \rfloor}{10^d}$$

where $x$ is the number to be rounded, $d$ is the number of decimal places to which $x$ should be rounded, and $t$ is the threshold for rounding up (e.g., $t = 5$ for rounding up from 5). Note that $\lfloor n \rfloor$ floors a number $n$, and $\lceil n \rceil$ ceils it.

Rounding down works accordingly. Note that $+$ and $-$ are reversed here:

$$\frac{\lceil x(10^d) - 1 + \frac{t}{10} \rceil}{10^d}$$

To even (base R)

Like Python’s round() function, R’s base::round() doesn’t round up or down, or use any other procedure based solely on the truncated part of the number. Instead, round() strives to round to the next even number. This is also called “banker’s rounding”, and it follows a technical standard, IEEE 754.

Realizing that round() works in a highly unintuitive way sometimes leads to consternation. Why can’t we just round like we learned in school, that is, up from 5? The reason seems to be bias. Because 5 is right in between two whole numbers, any procedure that rounds 5 in some predetermined direction introduces a bias toward that direction. Rounding up from 5 is therefore biased upward, and rounding down from 5 is biased downward.

As shown in the Rounding bias section below, this is unlikely to be a major issue when rounding raw numbers that originally have many decimal places. It might be more serious, however, if the initial number of decimal places is low (for whatever reason) and the need for precision is high.

At least in theory, “rounding to even” is not biased in either direction, and it preserves the mean of the original distribution. That is how round() aims to operate. Here is a case in which it works out, whereas the bias of rounding up or down is fully apparent:

vec1 <- seq(from = 0.5, to = 9.5)
up1 <- round_up(vec1)
down1 <- round_down(vec1)
even1 <- round(vec1)

vec1
#>  [1] 0.5 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5
up1
#>  [1]  1  2  3  4  5  6  7  8  9 10
down1
#>  [1] 0 1 2 3 4 5 6 7 8 9
even1
#>  [1]  0  2  2  4  4  6  6  8  8 10

# Original mean
mean(vec1)
#> [1] 5

# Means when rounding up or down: bias!
mean(up1)
#> [1] 5.5
mean(down1)
#> [1] 4.5

# Mean when rounding to even: no bias
mean(even1)
#> [1] 5

However, this noble goal of unbiased rounding runs up against the reality of floating point arithmetic. You might therefore get results from round() that first seem bizarre, or at least unpredictable. Consider:

vec2 <- seq(from = 4.5, to = 10.5)

up2 <- round_up(vec2)
down2 <- round_down(vec2)
even2 <- round(vec2)

vec2
#> [1]  4.5  5.5  6.5  7.5  8.5  9.5 10.5
up2
#> [1]  5  6  7  8  9 10 11
down2
#> [1]  4  5  6  7  8  9 10

even2  # No symmetry here...
#> [1]  4  6  6  8  8 10 10

mean(vec2)
#> [1] 7.5
mean(up2)
#> [1] 8
mean(down2)
#> [1] 7
mean(even2)  # ... and the mean is slightly biased downward!
#> [1] 7.428571


vec3 <- c(
  1.05, 1.15, 1.25, 1.35, 1.45,
  1.55, 1.65, 1.75, 1.85, 1.95
)

# No bias here, though:
round(vec3, 1)
#>  [1] 1.0 1.1 1.2 1.4 1.4 1.6 1.6 1.8 1.9 2.0
mean(vec3)
#> [1] 1.5
mean(round(vec3, 1))
#> [1] 1.5

Sometimes round() behaves just as it should, but at other times, results can be hard to explain. Martin Mächler, who wrote the present version of round(), describes the issue about as follows:

The reason for the above behavior is that most decimal fractions can’t, in fact, be represented as double precision numbers. Even seemingly “clean” numbers with only a few decimal places come with a long invisible mantissa, and are therefore closer to one side or the other. (To see this clearly, try entering a few decimal numbers on Float Exposed.)

We usually think that rounding rules are all about breaking a tie that occurs at 5. Most floating-point numbers, however, are just somewhat less than or greater than 5. There is no tie! Consequently, Mächler says, rounding functions need to “measure, not guess which of the two possible decimals is closer to x” — and therefore, which way to round.

This seems better than following mathematical intuitions that may not always correspond to the way computers actually deal with numbers. R has used the present solution since version 4.0.0.

base::round() can seem like a black box, but it seems unbiased in the long run. I recommend using round() for original work, even though it is quite different from other rounding procedures — and therefore unsuitable for reconstructing them. Instead, we need something like scrutiny’s round_*() functions.

IEEE 754 rounding standard

base::round() and some of scrutiny’s rounding functions correspond to the IEEE 754 rounding standard (IEEE 2019, pp. 27f.; the Wikipedia page is more accessible). IEEE 754 defines standards for floating-point operations, which includes rounding.

This table shows how base::round() and scrutiny correspond to IEEE 754:

Function	IEEE 754 attribute
base::round()	roundTiesToEven
round_up() with symmetric = TRUE	roundTiesToAway
round_ceiling()	roundTowardPositive
round_floor()	roundTowardNegative
round_trunc()	roundTowardZero

Admittedly, scrutiny’s rounding functions were written without this standard in mind. That is why their names don’t match those of the IEEE rounding procedures (or “rounding-direction attributes”), and why one of them requires the optional symmetric argument to meet the standard. A more straightforward mapping might be more desirable, and future breaking changes in a major version of scrutiny are not out of the question. However, other considerations apply, as well.

Reconstruct rounding bounds with unround()

Rounding leads to a loss of information. The mantissa is cut off in part or in full, and the resulting number is underdetermined with respect to the original number: The latter can’t be inferred from the former. It might be of interest, however, to compute the range of the original number given the rounded number (especially the number of decimal places to which it was rounded) and the presumed rounding method.

While it’s often easy to infer such a range, we better have the computer do it. Enter unround(). It returns the lower and upper bounds, and it says whether these bounds are inclusive or not — something that varies greatly by rounding procedure. Currently, unround() is used as a helper within scrutiny’s DEBIT implementation; see vignette("debit").

The default rounding procedure for unround() is "up_or_down":

unround(x = "8.0")
#> # A tibble: 1 × 7
#>   range                  rounding   lower incl_lower x     incl_upper upper
#>   <chr>                  <chr>      <dbl> <lgl>      <chr> <lgl>      <dbl>
#> 1 7.95 <= x(8.0) <= 8.05 up_or_down  7.95 TRUE       8.0   TRUE        8.05

For a complete list of featured rounding procedures, see documentation for unround(), section Rounding.

On the left, the range column displays a pithy graphical overview of the other columns (except for rounding) in the same order:

1. lower is the lower bound for the original number.
2. incl_lower is TRUE if the lower bound is inclusive and FALSE otherwise.
3. x is the input value.
4. incl_upper is TRUE if the upper bound is inclusive and FALSE otherwise.
5. upper is the upper bound for the original number.

By default, decimal places are counted internally so that the function always operates on the appropriate decimal level. This creates a need to take trailing zeros into account, which is why x needs to be a string:

unround(x = "3.50", rounding = "up")
#> # A tibble: 1 × 7
#>   range                    rounding lower incl_lower x     incl_upper upper
#>   <chr>                    <chr>    <dbl> <lgl>      <chr> <lgl>      <dbl>
#> 1 3.495 <= x(3.50) < 3.505 up        3.50 TRUE       3.50  FALSE       3.50

Alternatively, a function that uses unround() as a helper might count decimal places by itself (i.e., by internally calling decimal_places()). It should then pass these numbers to unround() via the decimals argument instead of letting it redundantly count decimal places a second time.

In this case, x can be numeric because trailing zeros are no longer needed. (That, in turn, is because the responsibility to count decimal places in number-strings rather than numeric values shifts from unround() to the higher-level function.)

The following call returns the exact same tibble as above:

unround(x = 3.5, digits = 2, rounding = "up")
#> # A tibble: 1 × 7
#>   range                   rounding lower incl_lower     x incl_upper upper
#>   <chr>                   <chr>    <dbl> <lgl>      <dbl> <lgl>      <dbl>
#> 1 3.495 <= x(3.5) < 3.505 up        3.50 TRUE         3.5 FALSE       3.50

Since x is vectorized, you might test several reported numbers at once:

vec2 <- c(2, 3.1, 3.5) %>% 
  restore_zeros()

vec2   # `restore_zeros()` returns "2.0" for 2
#> [1] "2.0" "3.1" "3.5"

vec2 %>% 
  unround(rounding = "even")
#> # A tibble: 3 × 7
#>   range                rounding lower incl_lower x     incl_upper upper
#>   <chr>                <chr>    <dbl> <lgl>      <chr> <lgl>      <dbl>
#> 1 1.95 < x(2.0) < 2.05 even      1.95 FALSE      2.0   FALSE       2.05
#> 2 3.05 < x(3.1) < 3.15 even      3.05 FALSE      3.1   FALSE       3.15
#> 3 3.45 < x(3.5) < 3.55 even      3.45 FALSE      3.5   FALSE       3.55

Fractional rounding

What if you want to round numbers to a fraction instead of an integer? Check out reround_to_fraction() and reround_to_fraction_level():

reround_to_fraction(x = 0.4, denominator = 2, rounding = "up")
#> [1] 0.5

This function rounds 0.4 to 0.5 because that’s the closest fraction of 2. It is inspired by janitor::round_to_fraction(), and credit for the core implementation goes there. reround_to_fraction() blends janitor’s fractional rounding with the flexibility and precision that reround() provides.

What’s more, reround_to_fraction_level() rounds to the nearest fraction at the decimal level specified via its digits argument:

reround_to_fraction_level(
  x = 0.777, denominator = 5, digits = 0, rounding = "down"
)
#> [1] 0.8
reround_to_fraction_level(
  x = 0.777, denominator = 5, digits = 1, rounding = "down"
)
#> [1] 0.78
reround_to_fraction_level(
  x = 0.777, denominator = 5, digits = 2, rounding = "down"
)
#> [1] 0.776

These two functions are not currently part of any error detection workflow.

Rounding bias

I wrote above that rounding up or down from 5 is biased. However, this points to a wider problem: It is true of any rounding procedure that doesn’t take active precautions against such bias. base::round() does, and that is why I recommend it for original work (as opposed to reconstruction).

It might be useful to have a general and flexible way to quantify how far rounding biases a distribution, as compared to how it looked like before rounding. The function rounding_bias() fulfills this role. It is a wrapper around reround(), so it can access any rounding procedure that reround() can, and takes all of the same arguments. However, the default for rounding is "up" instead of "up_or_down" because rounding_bias() only makes sense with single rounding procedures.

In general, bias due to rounding is computed by subtracting the original distribution from the rounded one:

$$bias = x_{rounded} - x$$

By default, the mean is computed to reduce the bias to a single data point:

vec3 <- seq(from = 0.6, to = 0.7, by = 0.01)

vec3
#>  [1] 0.60 0.61 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.70

# The mean before rounding...
mean(vec3)
#> [1] 0.65

# ...is not the same as afterwards...
mean(round_up(vec3))
#> [1] 1

# ...and the difference is bias:
rounding_bias(x = vec3, digits = 0, rounding = "up")
#> [1] 0.35

Set mean to FALSE to return the whole vector of individual biases instead:

rounding_bias(x = vec3, digits = 0, rounding = "up", mean = FALSE)
#>  [1] 0.40 0.39 0.38 0.37 0.36 0.35 0.34 0.33 0.32 0.31 0.30

Admittedly, this example is somewhat overdramatic. Here is a rather harmless one:

vec4 <- rnorm(50000, 100, 15)

rounding_bias(vec4, digits = 2)
#> [1] 1.254758e-05

What is responsible for such a difference? It seems to be (1) the sample size and (2) the number of decimal places to which the vector is rounded. The rounding method doesn’t appear to matter if numbers with many decimal places are rounded:

#> # A tibble: 10 × 3
#>             bias decimal_digits rounding
#>            <dbl> <chr>          <chr>   
#>  1 0.00000925    1 up           up      
#>  2 0.0000125     2 up           up      
#>  3 0.00000117    3 up           up      
#>  4 0.0000000596  4 up           up      
#>  5 0.00000000342 5 up           up      
#>  6 0.00000925    1 even         even    
#>  7 0.0000125     2 even         even    
#>  8 0.00000117    3 even         even    
#>  9 0.0000000596  4 even         even    
#> 10 0.00000000342 5 even         even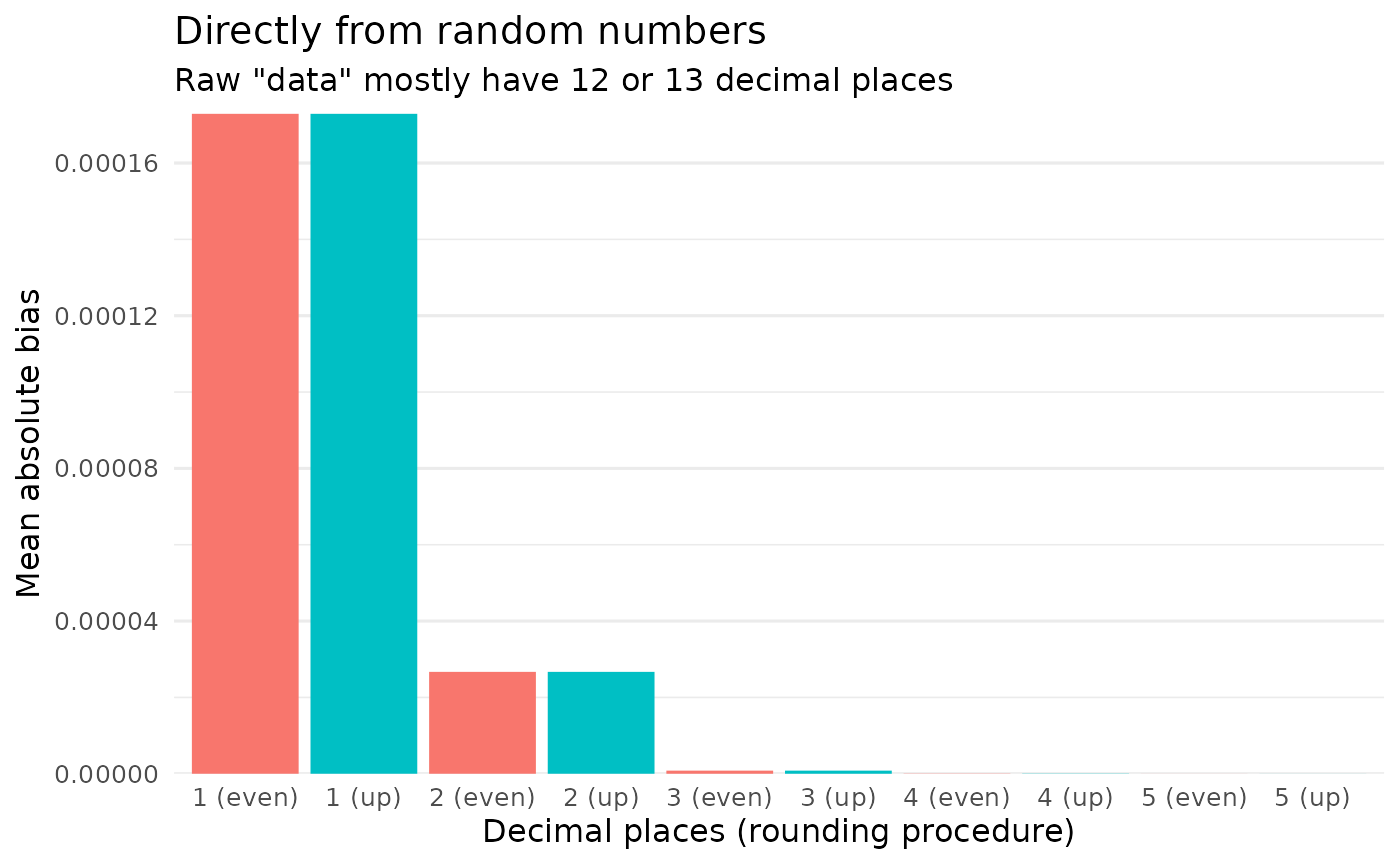

However, if the raw values are preliminarily rounded to 2 decimal places before rounding proceeds as above, the picture is different:

#> # A tibble: 10 × 3
#>         bias decimal_digits rounding
#>        <dbl> <chr>          <chr>   
#>  1 0.00491   1 up           up      
#>  2 0         2 up           up      
#>  3 0         3 up           up      
#>  4 0         4 up           up      
#>  5 0         5 up           up      
#>  6 0.0000178 1 even         even    
#>  7 0         2 even         even    
#>  8 0         3 even         even    
#>  9 0         4 even         even    
#> 10 0         5 even         even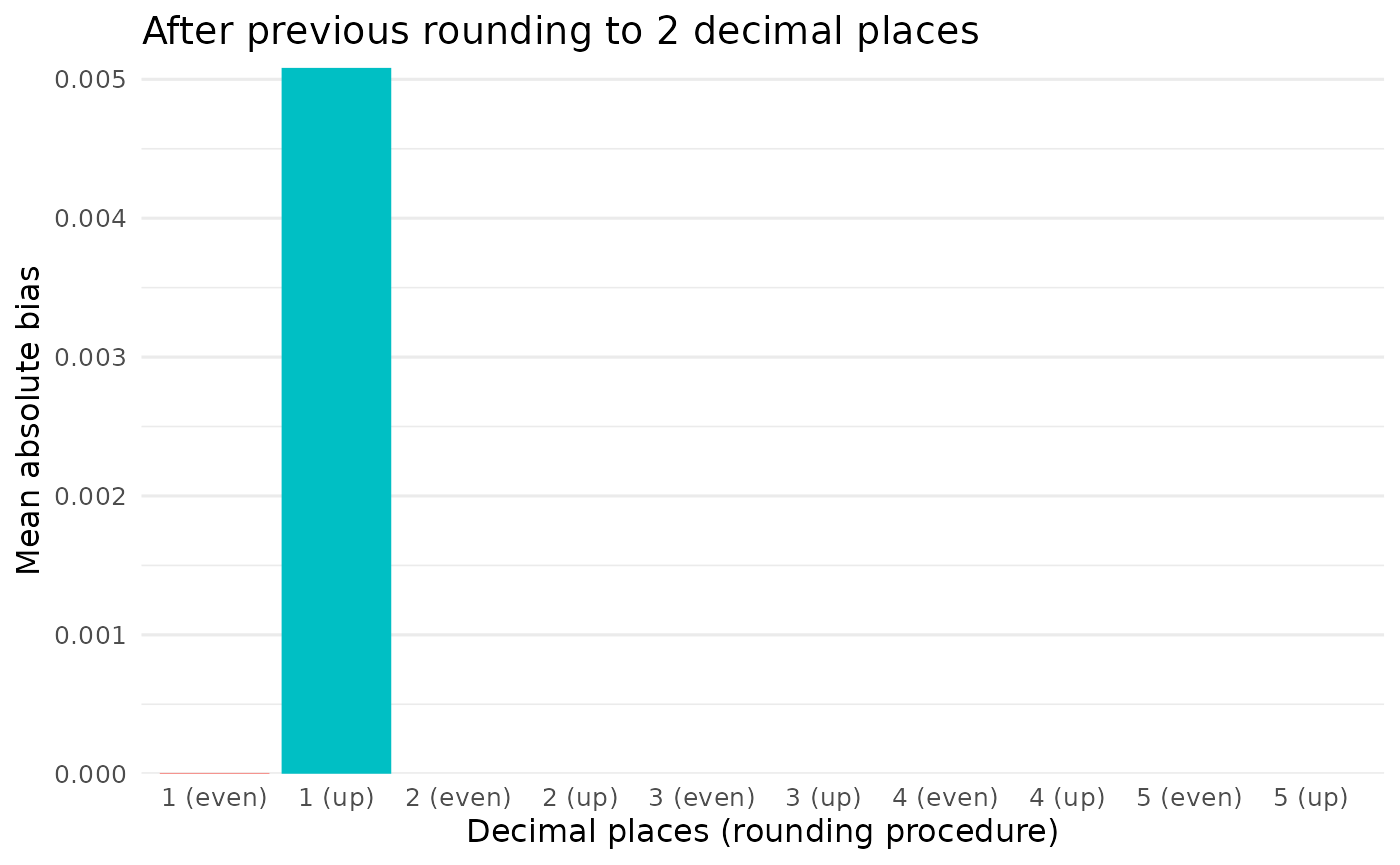

In sum, the function allows users to quantify the degree to which rounding biases a distribution, so that they can assess the relative merits of different rounding procedures. This is partly to sensitize readers to potential bias in edge cases, but also to enable them to make informed rounding decisions on their own.

Citation dummy

(Here is an extra section. Its display is suppressed via the CSS element display: none; because its only purpose is to generate the citation IEEE (2019) — I want to style the citation in the text above more flexibly than the format allows (without parentheses) but still get the reference pasted at the bottom.)

References

IEEE. 2019. “IEEE Standard for Floating-Point Arithmetic.” https://doi.org/10.1109/IEEESTD.2019.8766229.